Quando um professor entra na sala de aula e diz que iniciará o estudo dos números complexos, os alunos pensam que são números, no mínimo, muito complicados. Ao saber que também existem números chamados de imaginários os alunos dirão que tais números, por serem imaginários, não existem, e portanto, para que estudá-los?
Este texto pretende mostrar que não é bem assim. Percorrendo sua história veremos que o surgimento de tais números está intimamente ligado à resolução de equações algébricas.
O fato de um número negativo não ter raiz quadrada parece ter sido sempre claro para os matemáticos que se depararam com esta questão, até a concepção do modelo dos números complexos. Um número complexo é um número z que pode ser escrito na forma z = x + yi, sendo x e y números reais e i denota a unidade imaginária. Esta tem a propriedade i^2 = -1, sendo que x e y são chamados respectivamente parte real e parte imaginária de z.
O conjunto dos números complexos, denotado por C, contém o conjunto dos números reais. Munido de operações de adição e multiplicação obtidas por extensão das operações de mesma denominação nos números reais, adquire uma estrutura algébrica denominada corpo algebricamente fechado, sendo que esse fechamento consiste na propriedade que tem o conjunto de possuir todas as soluções de qualquer equação polinomial com coeficientes naquele mesmo conjunto (no caso, o conjunto dos complexos).
Os primeiros que conseguiram dar soluções a equações cúbicas foram Scipione del Ferro e Tartaglia. Este último, depois de ter sido alvo de muita insistência, passou os resultados que tinha obtido a Girolamo Cardano, que prometeu não divulgá-los. Cardano, depois de conferir a exatidão das resoluções de Tartaglia, não honrou sua promessa e publicou os resultados, mencionando o autor, em sua obra Ars Magna de 1545, iniciando uma enorme inimizade.
A fórmula deduzida por Tartaglia afirmava que a solução da equação  era dada por
era dada por
 era dada por
era dada por
Um problema inquietante percebido na época foi que algumas equações (as equações que tem três raízes reais, chamadas de casus irreducibilis) levavam a raízes quadradas de números negativos.
Por exemplo, a equação:
tem três raízes reais, como se pode observar facilmente ou pelo gráfico da função:
ou por fatoração:
se e somente se:
ou:
Entretanto, usando-se a fórmula de Tartaglia, chega-se a:
Essa questão evidenciou o fato de que havia mais a se investigar e a se aprender sobre os números.
Rafael Bombelli experimentou escrever as expressões:
![\sqrt[3]{2+\sqrt{-121}}](https://upload.wikimedia.org/math/3/f/e/3fee2772ddfd1328af3b966403bfb3f0.png) e
e ![\sqrt[3]{2-\sqrt{-121}}](https://upload.wikimedia.org/math/4/e/0/4e0b91f65306afdb82577a0d608b8041.png)
na forma:
 e
e 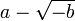
respectivamente. Admitindo válidas as propriedades usuais das operações tais como comutativa, distributiva etc., usou-as nas expressões obtidas, obtendo  e
e  Com isso, chegou a:
Com isso, chegou a:
 e
e  Com isso, chegou a:
Com isso, chegou a:
No início, os números complexos não eram vistos como números, mas sim como um artifício algébrico útil para se resolver equações. Descartes, no século XVII, os chamou de números imaginários.
Os números complexos são utilizados em várias áreas do conhecimento, tais como engenharia, eletromagnetismo, física quântica, teoria do caos, além da própria matemática, em que são estudadas análise complexa, álgebra linear complexa, álgebra de Lie complexa, com aplicações em resolução de equações algébricas e equações diferenciais.
Em algumas situações, é comum a troca da letra i pela letra j, devido ao frequente uso da primeira como indicação de corrente elétrica.
Fonte: Wikipédia

![x = \sqrt[3]{-\frac{q}{2} + \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}} + \sqrt[3]{- \frac{q}{2} - \sqrt{(\frac{q}{2})^2 +
(\frac{p}{3})^3}}.](https://upload.wikimedia.org/math/d/4/0/d40a53f0a19c385963fe4a7e455b725b.png)
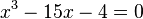


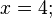
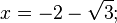

![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}}](https://upload.wikimedia.org/math/d/7/6/d760c016360c634b509a4b9eb6ffdbfa.png)
![x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}} = (2 + \sqrt{-1}) + (2 - \sqrt{-1}) = 4](https://upload.wikimedia.org/math/b/1/1/b117444fc7123d7aa30006178140af23.png)


