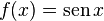Matemática - trigonometria : função seno e função cosseno ~ Concursos Exatas

Gráfico de f(x) = sen x

f(x) = \sen x

Associa a cada número real x o número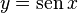

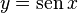
y = \sen x

Domínio: Como x pode assumir qualquer valor real: $D = R$
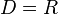
Conjunto Imagem: Como seno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: $\operatorname{Im} = [-1, 1]$
Gráfico: Ele sempre se repete no intervalo de 0 a $2\pi$ . Esse intervalo é denominado senóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Período: É sempre o comprimento da senóide. No caso da função 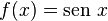$f(x) = \operatorname{sen}\, x$ , a senóide caracteríza-se pelo intervalo de 0 a $2\pi$ , portanto o período é 2 $\pi$ .
Paridade: Dado que sen (-x) = - sen x, a função seno é ímpar.
Sinal da Função: Como seno x é a ordenada do ponto-extremidade do arco:
- f(x) = sen x é positiva no 1° e 2° quadrantes (ordenada positiva).
- f(x) = sen x é negativa no 3° e 4° quadrantes (ordenada negativa).

Gráfico de f(x) = cos x

f(x) = \cos x

Associa a cada número real x o número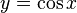

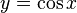
y = \cos x

Domínio: Como x pode assumir qualquer valor real: $D = R$
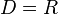
Conjunto Imagem: Como cosseno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: $\operatorname{Im} = [-1, 1]$
Gráfico: Ele sempre se repete no intervalo de 0 a $2\pi$ . Esse intervalo é denominado cossenóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Período: É sempre o comprimento da cossenóide. No caso da função f(x) = cos x , a cossenóide caracteriza-se pelo intervalo de 0 a $2\pi$ , portanto o período é $2\pi$ .
Paridade: Dado que cos (-x) = cos x, a função cosseno é par.
Sinal da Função: Como o cosseno x é a abscissa do ponto-extremidade do arco:

Fonte:Wikipédia.

Concursos Exatas